
생활 속에 스며 있는 수학적 원리들
오늘은 생활 속에 스며 있는 수학의 원리들을 알아보고자 한다. 음료수 캔이 원기둥인 이유를 아는가? 꿀벌은 왜 정육각형 모양으로 집을 짓는지 아는가? 생활 속에서 그저 당연하게 아무 생각 없이 느껴졌던 것들에 이유가 있었음을 이 시간에 정리해보고자 한다.
음료수 캔이 원기둥인 이유
각기둥 모양의 음료수 캔을 본 적이 있는가? 아마 없을 것이다. 상상해보자. 각기둥 모양의 음료수 캔... 꼭짓점이 뾰족하여 아플 것 같고, 그 뾰족한 부분으로 구멍이 잘 날 것 같다. 그러나 이것은 음료수 캔이 원기둥인 이유가 아니라 각기둥이 아닌 이유에 불과할 것이다. 그렇다면 정말 음료수 캔이 원기둥인 이유는? 바로 용기를 만드는데 드는 재료를 최소화할 수 있기 때문이다. 용기를 만드는 재료의 최소화는 원가비용과 연관이 있기에 수익과 연결되는 부분이다.
자. 그렇다면 왜 원기둥이 용기가 최소화 되는지 생각해보자.
원은 동일한 넓이를 갖고 있는 평면도형 중에서 둘레의 길이가 최소인 도형이다. 바꾸어 말하면 일정한 둘레를 지닌 평면도형 중에 최대 넓이를 지니고 있다.
이해되지 않을 수 있으니 예를 들어서 설명해보도록 하겠다.

정사각기둥과 원기둥의 두 입체도형을 생각해보자. 각각의 밑넓이를 100이라 생각하고 높이를 10이라 생각해보자.
그렇다면 부피는 밑넓이×높이 이므로 두 도형의 부피는 동일하다. 즉 두 도형에는 같은 양의 음료수가 담길 수 있는 것이다. 그러나 겉넓이에서는 차이가 발생한다. 겉넓이는 음료수를 만드는 재료가 들어가는 재료의 양이므로 겉넓이가 적을수록 만드는 회사에서는 이익이다.
겉넓이를 비교해 보도록 하자.
정사각기둥의 밑넓이가 100이므로 가로 세로는 각각 10이 된다. 옆넓이는 밑면의 둘레×높이 이므로 옆넓이는 400이 된다. 즉 겉넓이는 밑넓이×2+옆넓이 이므로 600이 되는 것이다.
원기둥의 겉넓이를 생각해보자. 밑넓이가 100이므로 원의 둘레는 약 35.4가 된다. 옆넓이는 원의둘레(원기둥의 밑면의 원이 옆넓이의 가로를 감싸므로)×높이가 된다. 즉 옆넓이는 354가 된다. 따라서 겉넓이는 밑넓이×2+옆넓이 이므로 554가 된다.
위의 결과를 정리하면 정사각기둥 겉넓이는 600, 원기둥 겉넓이는 554이다. 그러므로 재료를 덜 사용할 도형은 원기둥이므로 음료수 캔은 원기둥이 된 것이다.

꿀벌의 집이 정육각형인 이유
꿀벌은 왜 집모양이 정육각형일까? 정삼각형, 정사각형 등등 모양이 다양한데 왜 정육각형 모양의 집을 선택했을까? 자연의 동물들은 참 신비하다. 여기에는 꿀벌의 놀라운 신비가 숨겨져 있다.
테셀레이션이라고 들어보았는가? 테셀레이션은 도형을 이용하여 평면이나 공간을 완전히 메우는 것을 말한다. 이때 겹치거나 틈이 생기거나 하지 않게 늘어놓게 된다. 예를 들어 보자. 정삼각형 모양을 가지고 평면을 빈틈없이 그릴 수 있는가? 그릴 수 있다. 정사각형과 정육각형도 가능하다.
정다각형 중에서 평면을 빈틈없이 메울 수 있는 것은 이 정삼각형, 정사각형, 정육각형 세 가지 뿐이다.
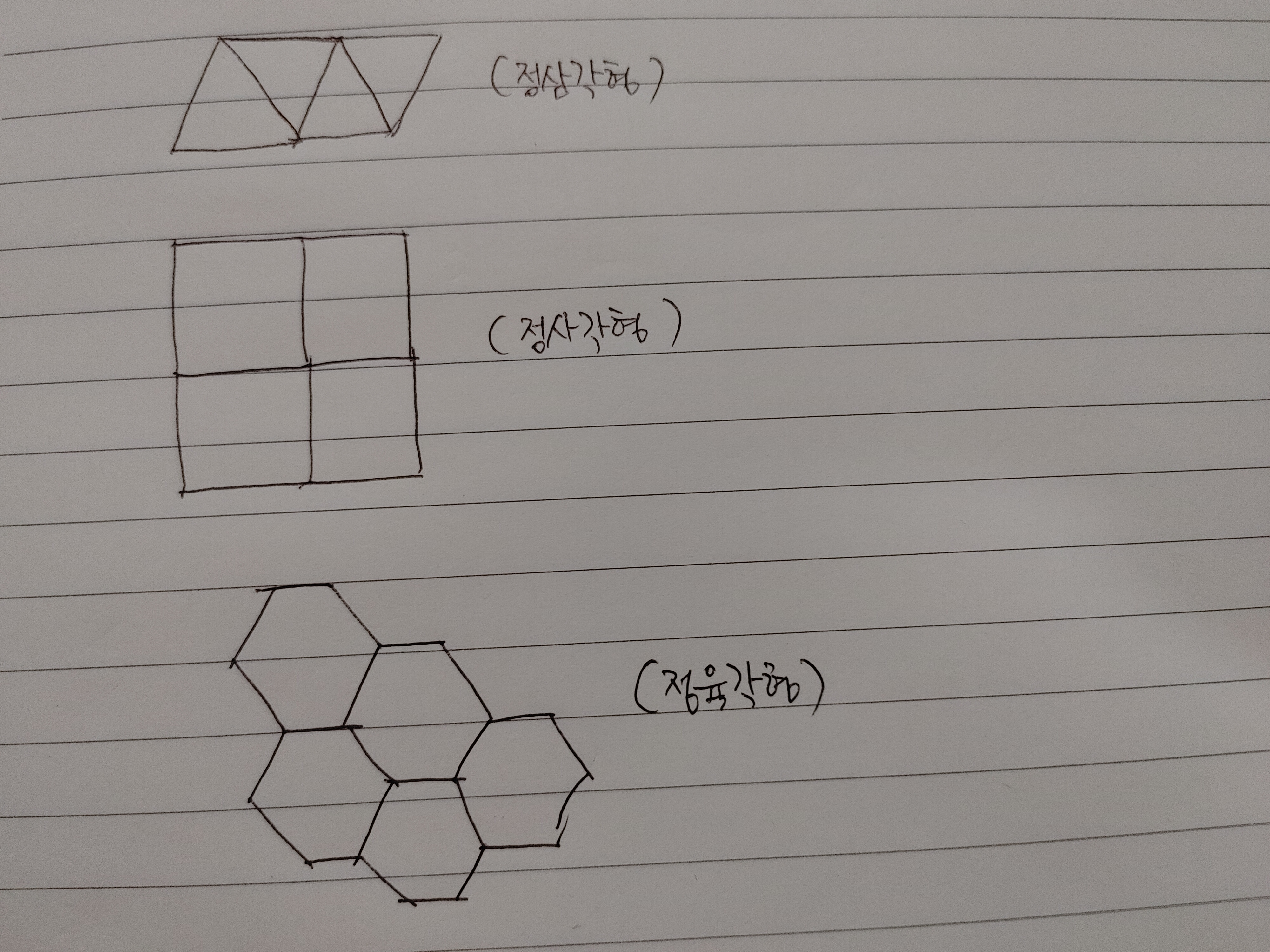
그렇다면 꿀벌은 이들 중 왜 정육각형 모양을 선택했을까?
답부터 이야기하자면 정육각형 모양의 벌집에 많은 꿀을 담을 수 있기 때문이다. 실은 같은 양의 재료를 가지고 가장 넓은 공간을 만들 수 있는 것은 원이다. 즉 원기둥 모양으로 벌집을 만들면 가장 많은 양의 꿀을 담을 수가 있다. 그러나 이 모양은 빈틈이 발생하기에 안정적인 면에서는 부족한 모양이다.
그렇다면 정삼각형 모양은 어떨까? 정삼각형 모양은 튼튼한 집을 지을 수는 있지만 동일한 공간을 만드는 데 정육각형 보다 두 배의 재료가 들어간다. 그리고 정사각형 모양은 어떨까? 이 경우에는 양 옆에서 건드려도 잘 흔들리기에 외부 힘에 쉽게 무너질 수 있다.
따라서 넓은 공간을 가지며, 구조가 안정적인 것은 바로 이 정육각형 모양인 것이다.
곤충조차 이런 수학적인 원리 안에 집을 짓고 있다니 놀라운 일이다.
정육각형의 또 다른 예
자연에서 정육각형이 이용되는 것에는 또 다른 예가 있다. 곤충의 눈과 잠자리의 날개, 그리고 하늘에서 내리는 눈에서 정육각형 모양의 결정체를 발견할 수 있다. 또한 비행기 날개 표피 재료의 내부도 이 정육각형 모양이고, 베개는 습도 조절을 위해 내부를 정육각형 모양으로 만들었다고 한다. 고속열차 앞부분 또한 정육각형을 연결시킨 모양의 충격흡수장치가 부착되어 있다고 한다.
이렇게 오늘은 자연 속에서 수학의 원리가 어떻게 숨겨져 있는지 알아보았다. 다음 시간에도 또 다른 수학 이야기로 찾아오고자 한다.
'수학 > 실생활 수학' 카테고리의 다른 글
| 생활 속 수학이야기7-생활 속의 숫자 이야기 (1) | 2021.06.01 |
|---|---|
| 생활 속 수학이야기6-꽃잎 수의 비밀 피보나치 수열 (0) | 2021.05.30 |
| 생활 속 수학 이야기4- 음수의 탄생 (0) | 2021.05.25 |
| 생활 속 수학이야기3-방정식에 관하여 (0) | 2021.05.24 |
| 생활 속 수학 예시 - 소수(+메르센 소수) (0) | 2021.05.21 |