어떤 축을 기준으로 반원을 회전시켰을 때 만들어지는 입체도형을 '구 '라고 부릅니다. 쉽게 생각하면 축구공, 지구본 등과 같은 모양을 '구'라고 합니다. 이때 가운데 위치하는 점을 '중심'이라고 부르고, 이 '중심'과 구 위의 한 점을 연결한 선분을 '반지름'이라고 합니다. 이 글에서는 구 겉넓이 공식과 부피 공식을 정리해 보도록 하겠습니다.
구 겉넓이 공식
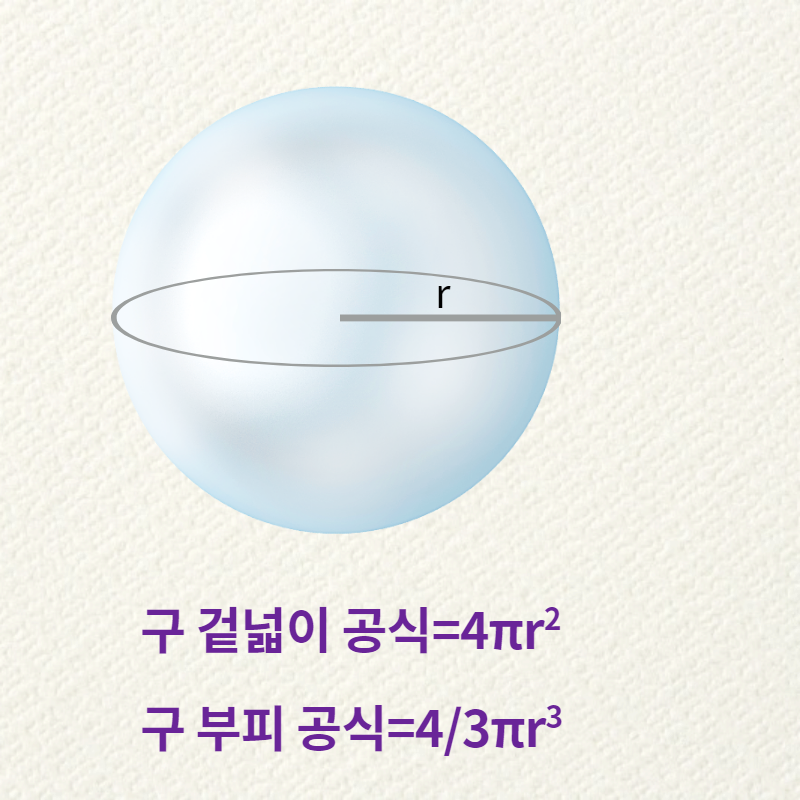
구 겉넓이 공식은 구의 겉표면에 색칠을 한다고 생각하면 됩니다. 반지름의 길이가 r인 구의 겉넓이를 구해보도록 하겠습니다. 이를 증명하기 위하여 털실을 이용하여 구의 겉을 감습니다. 이렇게 구 겉면을 다 감은 털실을 풀어서 바닥에 원 모양으로 돌돌 말아서 둡니다. 그러면 반지름의 길이가 2r인 원이 나옵니다. 즉 구 겉넓이는 반지름의 길이가 2r인 원의 넓이와 같다고 할 수 있습니다. 즉, 겉넓이는 4πr²이 나옵니다.
- 구 겉넓이 공식= 4πr²
구 겉넓이와 관련된 실생활 이야기를 다른 포스팅에 남겨두었으니 참고해주시면 좋겠습니다.
생활 속 수학 이야기15-구의 겉넓이 예
회전체와 구 오늘은 '구'에 대한 이야기를 해보려고 해요. 축구공, 지구본, 야구공 등과 같은 모양을 우리는 '구'라고 부르는데요. 회전체라는 것이 무엇인지, 그리고 회전체의 일종인 '구'에 대
tyrannohaha.com
구 부피 공식
구 부피를 구하기 위하여 원기둥을 이용합니다. 원기둥 안에 구를 쏙 넣어봅니다. 그러면 원기둥은 반지름은 r이고 높이는 2r인 원기둥이됩니다. 이 원기둥 안에 물을 담습니다. 그리고 그 안에 구를 넣었다가 빼봅니다. 그러면 흘러넘친 물의 양은 구의 부피라고 할 수 있습니다. 물은 원기둥의 높이의 2/3 만큼이 빠져나갔습니다. 따라서 원기둥 부피의 2/3 만큼이 구의 부피라고 할 수 있습니다.
이 방식을 이용하면 구 부피는 2/3×원기둥 부패=2/3×πr^2×2r=4/3πr^3 이라고 할 수 있습니다.
- 구 부피 공식=4/3πr^3
오늘은 구 겉넓이 공식과 구 부피 공식을 정리해보았습니다. 도움이 되셨기를 바랍니다.
'수학 > 중1 수학' 카테고리의 다른 글
| 원기둥 부피 공식과 원뿔 부피 공식 정리 (0) | 2022.12.02 |
|---|---|
| 원둘레 공식(원주 구하는 공식)과 원 넓이 공식 정리 (0) | 2022.09.14 |
| 평행사변형 넓이 공식/ 사다리꼴 넓이 공식 / 마름모 넓이 공식 정리 (0) | 2022.09.09 |
| 삼각뿔 부피 공식, 사각뿔 부피 공식 정리!! (0) | 2022.09.08 |
| 중1 수학 목차 알아보고 공부 시작해봐요 (0) | 2021.07.06 |