함수라는 것은 x의 값에 따라 오직 하나의 y값이 정해지는 것을 말합니다. 이차함수라는 것은 x에 대한 이차식에 의하여 y값이 오직 하나 정해질 때를 말하는데요. 이차함수는 그래프 모양이 위로볼록하거나 아래로 볼록한 형태를 가지게 되고 다양한 특징들이 나타납니다. 이 글에서는 이차함수 그래프 유형을 모두 정리하고 성질들도 알아보도록 하겠습니다.
이차함수 뜻
이차함수라는 것은 y가 x에 대한 2차식으로 표현될 때 이차함수라고 합니다.
즉, y=ax²+bx+c에서 a≠0 일 때 이를 이차함수라고 부릅니다.
이차함수는 그래프로 그리면 아래로 볼록하고, 위로 볼록한 형태로 표현되는데요.
이러한 곡선을 포물선이라고 부릅니다.
이 포물선은 하나의 선으로 접으면 좌우대칭으로 접히고, 이 선을 우리는 축이라고 부릅니다.
또한 포물선과 축과의 교점을 꼭짓점이라 부릅니다.
y=ax² 의 그래프
y=ax² 그래프가 어떠한 특징을 가지는지 알아보도록 하겠습니다.
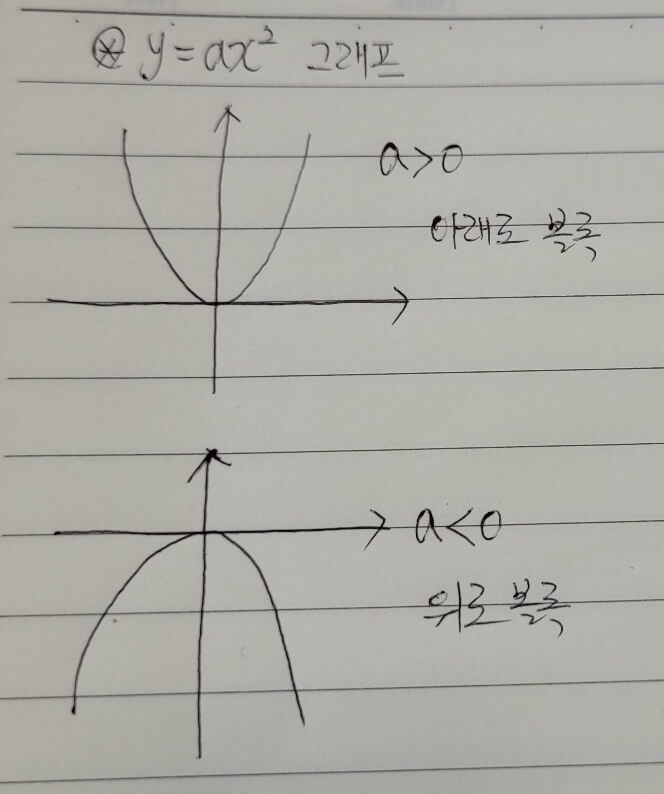
- 꼭짓점 : 원점(0,0)
- 축의 방정식 : x=0 (y축)
- a>0 : 아래로 볼록
a <0 : 위로 볼록 - a의 절댓값 : a의 절댓값이 클수록 y축에 가깝다.(폭이 좁아진다.)
y=ax²+q의 그래프
y=ax²+q의 그래프는 y=ax² 를 y축 방향으로 q만큼 평행이동 시킨 그래프입니다.
그래프가 좌우로 이동하는 것이 아니라 축은 변함없이 위아래로 이동했기에 축의 방정식은 그대로이고, 꼭짓점의 y좌표만 변화합니다.
- 꼭짓점 : (0, q)
- 축의 방정식 : x=0 (y축)
y=a(x-p) ² 의 그래프
y=ax² 를 x축으로 p만큼 평행이동 시킨 그래프입니다.
x축으로 p만큼 이동시켰기 때문에 축이 이동한 것이므로 축의 방정식이 바뀌고, 꼭짓점의 x좌표만 변화합니다.
- 꼭짓점 : (p,0)
- 축의 방정식 : x=p
y=a(x-p) ²+q의 그래프-이차함수의 표준형
y=ax²+q와 y=a(x-p)² 의 경우를 모두 적용시켰습니다.
즉 y=ax² 를 x축으로 p만큼, y축으로 q만큼 평행이동 시킨 그래프입니다.
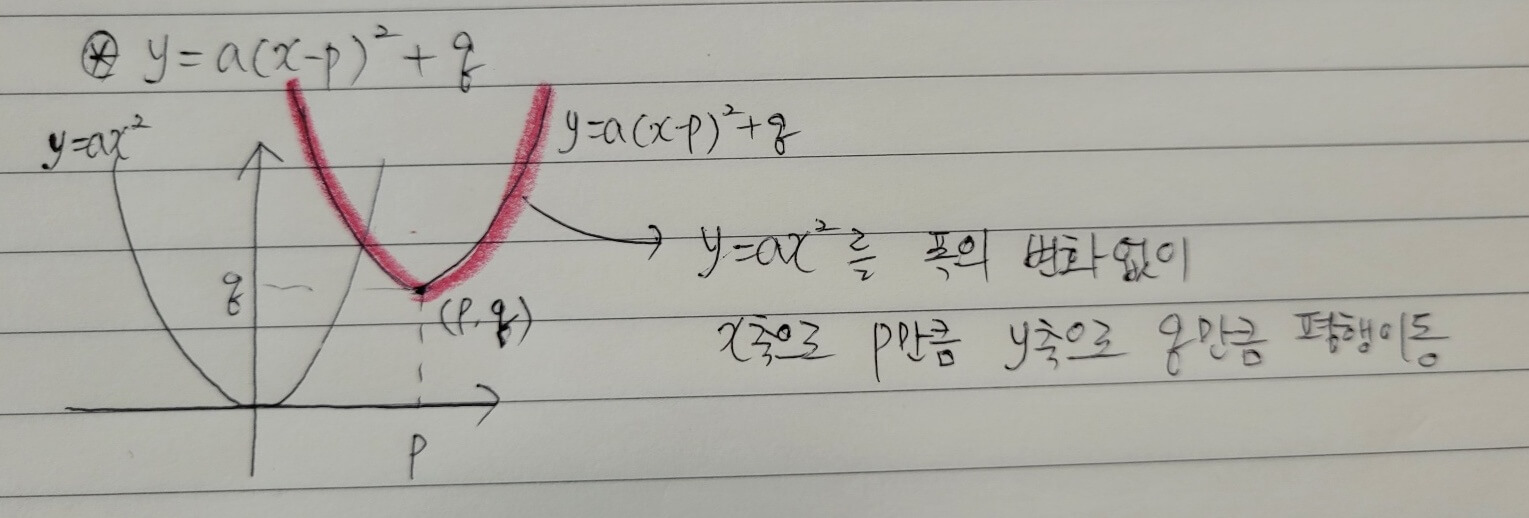
- 꼭짓점 : (p, q)
- 축의 방정식 x=p
여기에서 나오는 a, p, q의 부호에 대한 의미를 알아보겠습니다.
- a부호 : 그래프의 모양
a>0 : 아래로 볼록, a <0 : 위로 볼록 - p, q의 부호 : 꼭짓점의 위치를 결정
y=ax²+bx+c의 그래프
위의 형태의 그래프는 완전제곱식을 이용하여 이차함수의 표준형 y=a(x-p) ²+q꼴로 바꾸어 생각합니다.
완전제곱식으로 바꾸는 표준형으로 바꾸지 않고도 알 수 있는 성질이 있습니다.
y=ax²+bx+c이 가지고 있는 성질과 의미를 정리해 보겠습니다.
- a부호 : 그래프의 모양
a>0 : 아래로 볼록, a <0 : 위로 볼록 - b부호 : 축의 위치를 결정함 (좌동우이로 암기합니다. 즉, 왼쪽이면 a, b부호가 같고, 오른쪽이면 다르다.)
- 축이 y축의 왼쪽에 위치 : a와 b 부호는 동일
- 축이 y축 : b=0
- 축이 y축의 오른쪽에 위치 : a와 b는 다른 부호
- c부호 : y절편
지금까지 이차함수 그래프의 모양과 특성들을 정리해 보았습니다.
이차함수도 이차방정식에서 배웠던 완전제곱 형태로 바꾸는 과정을 하지 못하면 문제 푸는 것이 어렵습니다. 이차함수가 이해되지 않는다면 이차방정식의 완전제곱꼴로 바꾸는 부분에 대한 학습을 보강하면 좋겠습니다.
'수학 > 중3 수학' 카테고리의 다른 글
| 인수분해 공식 알아보고 그 개념 알기! (0) | 2023.03.08 |
|---|---|
| 분모의 유리화 하는 이유와 방법은? (0) | 2023.03.07 |
| 무리수와 실수 뜻/성질 정리해볼까요?(+무리수 소수 부분) (0) | 2023.01.02 |
| 제곱근 뜻과 성질, 루트 표현 알아볼까요? (0) | 2022.12.29 |
| 이차방정식 판별식 D와 그 뜻은? (+짝수 판별식) (0) | 2022.11.24 |