
수학자 오일러의 생애
오늘은 수학자이면서 물리학자이기도 한 오일러를 만나보고자 한다. 우선 오일러의 생애부터 알아보도록 하자.
오일러는 1707년 스위스의 바젤에서 목사의 아들로 태어났다. 오일러는 어린 시절부터 특출 나게 암기력도 좋고, 계산력과 언어능력이 뛰어났다고 한다. 그러나 그의 아버지는 오일러가 자신과 같이 목사가 되기를 원하였다. 그래서 14살에 스위스 명문 대학인 바젤 대학교에서 신학과 히브리어를 배우게 된다. 그러나 오일러는 수학자가 될 운명이었던 것일까? 바로 그곳에서 유명한 수학자인 요한 베르누이를 만나게 된다. 베르누이의 아들이 있었는데 그의 이름은 다니엘이었다. 다니엘과 오일러는 친하게 지내면서 수학을 더 열심히 했다고 한다. 그는 스승인 베르누이에게 질문하기보다는 스스로 문제를 해결하려고 노력을 많이 했다고 한다.
오일러는 바젤 대학의 수학 교수가 되기를 바랐지만 그 꿈을 이루지는 못했다고 한다. 수학의 천재여도 교수가 되는 것은 다른 문제인가 보다. 오일러는 개인사에서 불행한 일들을 많이 겪었다. 두 번 결혼하여 13명의 자녀를 낳았지만 이 중 8명은 오일러보다 먼저 하늘로 보냈으니 말이다. 그리고 수학을 너무 열심히 한 나머지 28살에 한쪽 눈을 실명하였고, 63세에는 다른 눈도 실명하게 된다. 그러나 놀라운 사실. 그는 두 눈이 모두 실명이 되었지만 두 눈이 멀게 된 이후에도 많은 논문을 쓰게 된다. 그의 수학에 대한 열정을 느낄 수 있는 바이다.큰 화재로 목숨을 잃을 뻔도 하였고, 69세에는 그의 아내가 먼저 하늘로 가는 불행도 겪는다. 그는 76세의 나이로 죽고 만다.
오일러 공식
우리가 도형 파트에서 오일러 공식을 배운 기억이 있을 것이다.

구와 연결 상태가 같은 다면체에서 v-e+f=2 라는 식.
여기에서 v는 꼭짓점의 개수, e는 모서리의 개수, f는 면의 수를 말한다.
(여기에서 구와 연결 상태가 같은 다면체라는 것을 조금 다르게 설명하고자 한다. 예를 들어보자. 정육면체 모양을 상상해보라. 여기에 공기를 주입시킨다고 생각해보자. 정육면체가 부풀면 구 모양이 될 수 있을 것 같은가? 맞다. 될 것 같다. 이런 것을 바로 구와 연결 상태가 같다고 봐도 좋다.)
오일러에 관한 이야기

1) 수학은 복잡한 식을 간단하게 나타낸다. 우리가 이렇게 간단하게 나타내게 된 이유가 바로 오일러 덕분이다. 예를 들어보자. 각을 대문자 A로 나타내고, 변을 소문자 a로 나타내게 된 것, 내접원 반지름을 소문자 r로 나태내고 외접원 반지름을 대문자 R로 표시한 사람이 바로 오일러이다.
그리고 고등학교에서 배우는 수. 바로 허수의 기호 i 또한 오일러가 사용하였다. 또한 함수의 기호인 f(x)도 오일러가 먼저 사용한 기호이다. 이 기호의 사용으로 우리는 수학을 보다 간결하게 나타낼 수 있게 되었다.
2) 대학 시절 이산수학을 배운 적이 있다. 그때 풀었던 문제. (물론 고등학교 시절에도 나왔었지만.)
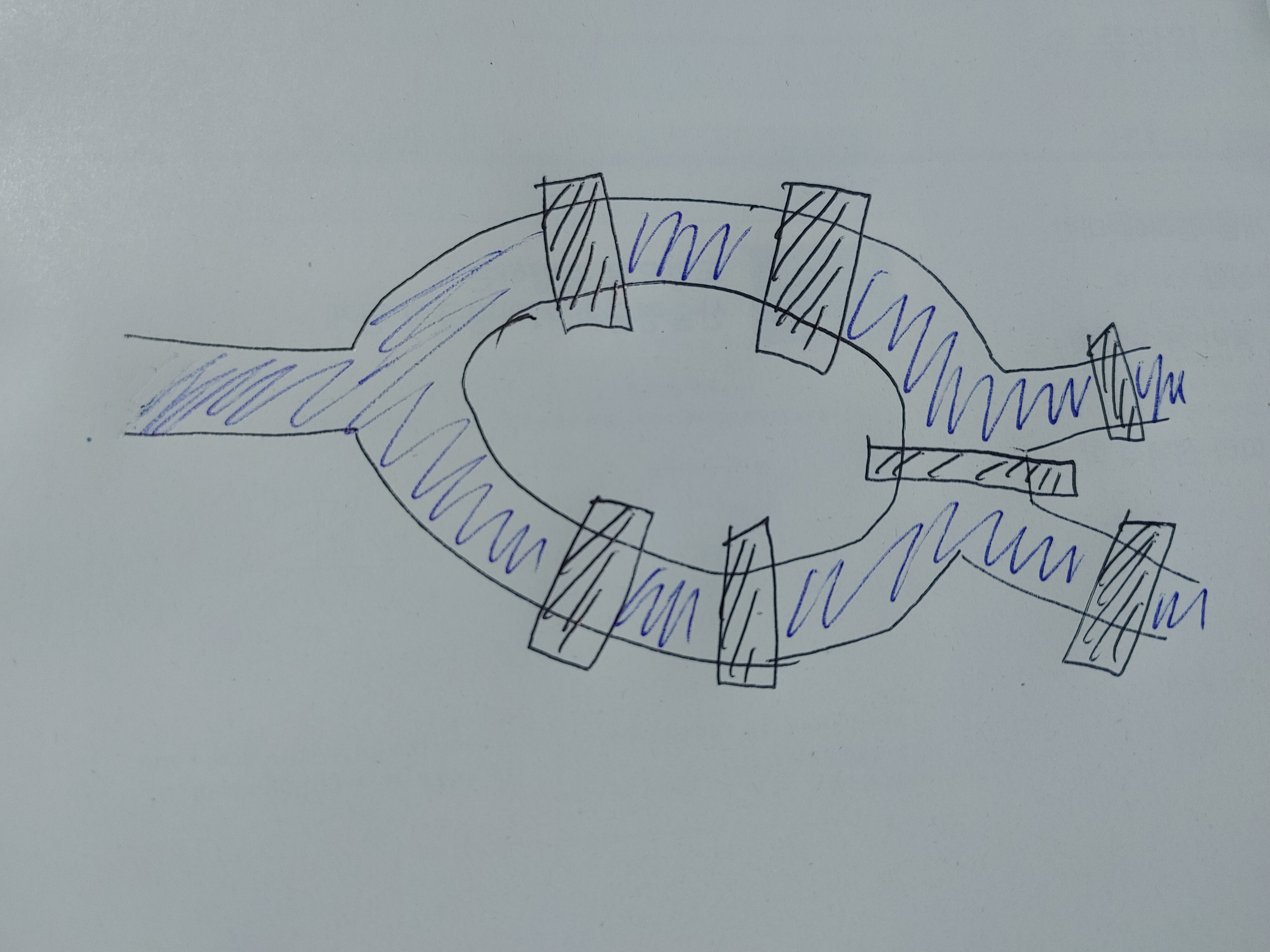
칸트라는 철학자의 고향인 쾨니히스베르그라는 도시에는 프레겔 강이 있다고 한다. 이 강에는 7개의 다리가 놓여 있었는데 당시 사람들은 같은 다리를 두 번 이상 건너지 않고 산책할 수 있는 방법을 찾으려고 했다고 한다. 그런데 이 문제를 많은 사람들이 해결하고 있지 못할 때 오일러가 이 문제를 해결했다고 한다.
땅을 점으로 다리를 선으로 바꿔서 연필을 떼지 않고 모든 선을 한 번 지나도록 그림을 그릴 수 있느냐의 문제로 바꿔서 다리를 두 번 이상 건너지 않고 산책할 수 있는 방법은 없다는 것을 설명했다고 한다. 이때 그린 점과 선분으로 이루어진 도형을 그래프라고 불렀고, 이 그래프 이론은 위상수학이라는 새로운 수학 분야를 탄생시킨다.
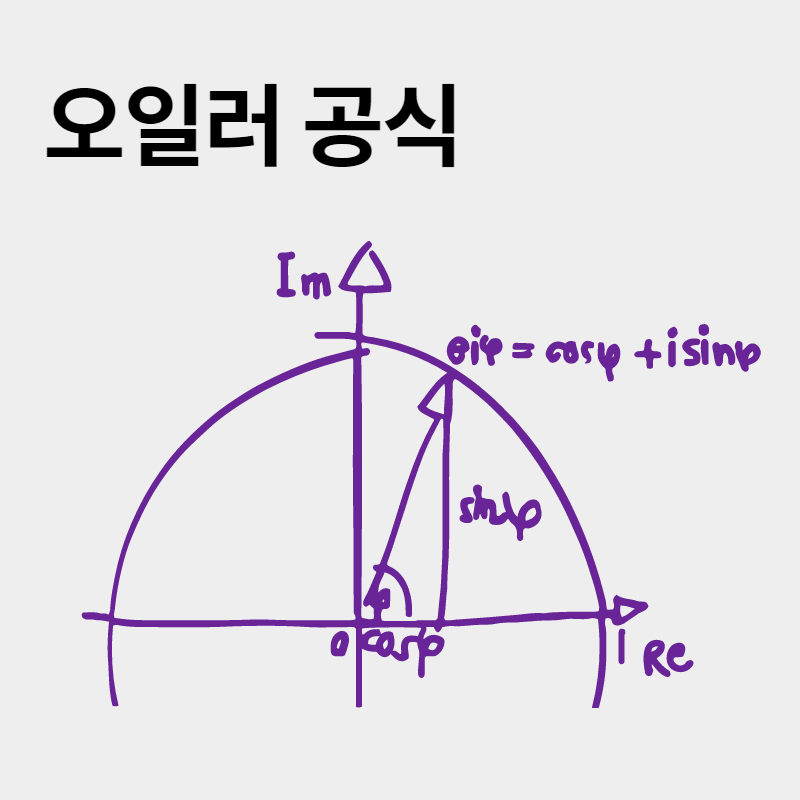
3) 오일러 공식
복소수의 지수를 정의할 때 사용되며 삼각함수와 지수함수에 대한 관계를 설명한다. 여기에서 실수 x에 대하여 허수 지수 ix를 위 그림 같이 정의했다. 이 식을 가장 아름다운 공식이라고 부르는 수학자도 있다.
지금까지 수학자 오일러의 삶과 그가 남긴 업적에 대하여 정리해 보았다. 수학자 이야기를 연재하면서 느끼는 점은 많은 수학자들의 삶이 각자 나름의 힘듦과 어려움이 있었지만 수학에 대한 사랑과 끈을 놓지 않고 꾸준히 연구했다는 집념이 있었다는 것이다. 그러면 다음 시간에 또 다른 수학자를 만나서 새로운 수학 세계를 만나도록 하자.
'수학 > 수학자' 카테고리의 다른 글
| 수학자 이야기6-페르마의 마지막 정리를 남긴 페르마 (0) | 2021.05.28 |
|---|---|
| 수학자 이야기5- 좌표평면 데카르트 (0) | 2021.05.26 |
| 수학자 이야기3-파스칼 (0) | 2021.05.22 |
| 등차수열 합공식과 수학자 가우스의 생애 정리 (0) | 2021.05.20 |
| 피타고라스의 정리- 수학자 피타고라스 일생 (0) | 2021.05.19 |